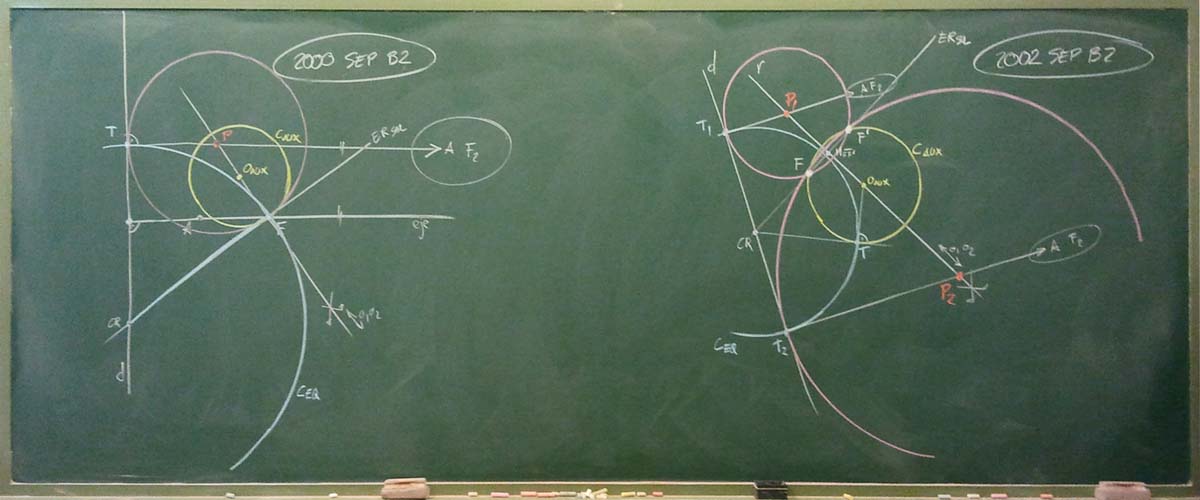Teoría: Definición de curvas cónicas

Una curva cónica es el resultado de la intersección de un plano con una superficie cónica. Según el ángulo que forman el plano y la superficie cónica, obtendremos una circunferencia, una elipse, una parábola o una hipérbola.


1º Definiciones sin circunferencias focales:

Circunferencia: Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.

Elipse: Lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.

Parábola: Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

Hipérbola: Lugar geométrico de los puntos del plano cuya diferencia de distancias a dos puntos fijos llamados focos es constante.


2º Definiciones con circunferencias focales:

Circunferencia: No tiene sentido usar esta definición.

Elipse: Lugar geométrico de los centros de las circunferencias que pasan por un punto fijo llamado foco uno y son tangentes interiores a una circunferencia fija llamada focal dos.

Parábola: Lugar geométrico de los centros de las circunferencias que pasan por un punto fijo llamado foco y son tangentes a una recta fija llamada directriz.

Hipérbola: Lugar geométrico de los centros de las circunferencias que pasan por un punto fijo llamado foco uno y son tangentes exteriores a una circunferencia fija llamada focal dos.

Teoría: Tangencias

Izquierda: Caso 03 de Apolonio (PRR)

Izquierda y Derecha: Caso 04 de Apolonio (RRR)

Ejercicio PAU: Curvas Cónicas

Izquierda: 2001 SEP B1
Derecha: 2002 JUN A2 y 2003 JUN A2

Izquierda y Centro: 2003 MOD A2

Roboscratch v0.03

Utiliza las flechas para mover el robot azul. El resto de las funciones están programadas.

Ejercicio PAU: Curvas Cónicas

Ejercicio PAU: Secciones Planas e Intersecciones

Ejercicio PAU: Curvas Cónicas

Teoría: Tangencias

2007 MOD A3: Elipse y 2012 SEP B1: Elipse

Se trata de un caso de intersección entre una recta y una elipse, pero podemos reducir el problema al Caso 09 de Apolonio (PPC):

2001 SEP A2: Elipse

Se trata de un caso de intersección entre una recta y una elipse, pero podemos reducir el problema al Caso 09 de Apolonio (PPC)

2011 MOD B1: Parábola

2009 MOD A3: Parábola

Se trata de un caso de intersección entre una recta y una parábola, pero podemos reducir el problema al Caso 02 de Apolonio

2002 SEP B2: Parábola

Se trata de un caso de intersección entre una recta y una parábola, pero podemos reducir el problema al Caso 02 de Apolonio

2000 SEP B2: Parábola

2000 SEP B2
Se trata de un caso de intersección entre una recta y una parábola, pero podemos reducir el problema al Caso 02 de Apolonio (PPR):

Ejercicio PAU: Tangencias

Izquierda: 2009 MOD A2
Derecha: 2009 MOD B2 y 2009 JUN A2

Izquierda: 2001 JUN B2, 2012 MOD 9 A1 y 2013 MOD A1
Derecha: 2003 MOD B2 y 2005 JUN A2

Izquierda: 2005 SEP A2
Derecha: 2008 JUN A2 y 2012 JUN  B1

Izquierda: 2010 JUN  FG A1

Izquierda: 2002 JUN B2 y 2007 JUN A2
Centro: 2010 JUN FE B1
Derecha: 2009 SEP A2

Teoría: Potencia y eje radical

Potencia de un punto respecto a una circunferencia:

Izquierda: Eje radical de dos circunferencias. Método de las tangentes exteriores.
Derecha: Eje radical de dos circunferencias. Método de la cincunferencia auxiliar.

Teoría: Rectas tangentes a una y dos circunferencias

Izquierda y derecha: Rectas tangentes a una circunferencia desde un punto exterior:

Izquierda: Recta tangente a una circunferencia desde un punto propio (el problema no tendría sentido si el punto es interior a la circunferencia):
Derecha: Rectas tangentes exteriores a dos circunferencias. Método de reducción:

Izquierda: Rectas tangentes interiores a dos circunferencias. Método de ampliación:

Teoría: Tangencias y enlaces

Diferencia entre TANGENCIA y ENLACE:

Propiedades de las tangencias:

2008 MOD A3: Apolonio

Ejercicio PAU: Tarjetas

Izquierda: 2011 JUN B2 y 2012 MOD 3 B2 (se trata del mismo ejercicio)
Derecha: 2009 MOD B1

Ejercicio PAU: Intersecciones

Izquierda: Intersección de una recta - pirámide.

Ejercicio PAU: Intersecciones

Izquierda: 2008 JUN B2

Ejercicio PAU: Intersecciones

Izquierda: 2012 MOD 2 B2
Derecha: 2002 JUN B3